编译过程
-
词法分析
识别出句子中的一个个单词,对构成源程序的字符串进行扫描和分解,识别出单词符号。
依循的原则:构词规则
描述工具:有限自动机
-
语法分析
分析句子的语法结构,根据语法规则把单词符号串分解成各类语法单位
依循的规则:语法规则
描述工具:上下文无光法
-
中间代码产生
根据句子的含义进行初步翻译
依循的规则:语义规则
描述工具:属性文法
-
优化
对译文进行修饰
依循的原则:程序的等价变换
-
目标代码的产生
写出最后的译文,其依赖于硬件系统结构和机器指令的含义
目标代码的三种形式:
- 汇编指令代码:需要进行汇编
- 绝对指令代码:可直接运行
- 可重新定位指令代码:需要连接
语义
一组规则,用它可以定义一个程序的意义
描述方法:
- 自然语言描述
- 二义性、隐藏错误,不完整性
- 形式描述
- 操作语义
- 指称语义
- 代数语义
以下是不是语义定义
- 类的声明必须以class开头(❌,这是对形式上的要求或规定)
- 关于函数调用时参数传递方法的描述(✔️)
标识符和名字
标识符:以字母开头的,由字母数字组成的字符串
名字:标识程序中的对象
只有当标识符与程序中的某个对象联系在一起的时候,才构成名字
举例:
Jordan(标识符)可能是篮球明星或者一个国家
当其与篮球明星挂钩时,才能表示乔丹(名字)
当其与国家挂钩时,才表示Jordan国家(名字)
一个字集的闭包和正则闭包 \(V^{0}=\{\epsilon\}\) 相等时:V中原来没有空字时,闭包($V^* = V····V$)会有空字,而正规闭包($V^+ = V V^*$)不会有空字
例子:
设U={a,aa},则$U^* = {\epsilon,a,aa,aaa,aaaa…}$,$U^+ = {a,aa,aaa,aaaa…}$
现在可以引出上下文无关法。
上下文无关法
\[G=(V_T,V_N,S,P)\]其中,$V_T$为终结符,$V_N$非终结符,$S$文法的开始符号,$P$为产生式


小故事:巴克斯范式(BNF)
句型,句子和语言

- 通过句子能推出最后的英文,所以最后的英文为句型
- 句子本身也是句型
- 掌握了所有语言的句子就掌握了这门语言,故“把语言定义为句子的全体”符合我们的认识

二义性
有文法二义性和语言二义性,语言二义性更强
只要语言存在一个文法非二义性,则语言就是非二义性的。
一个语言是二义的是指我们根本找不到一个能产生该语言的无二义文法。

词法分析器
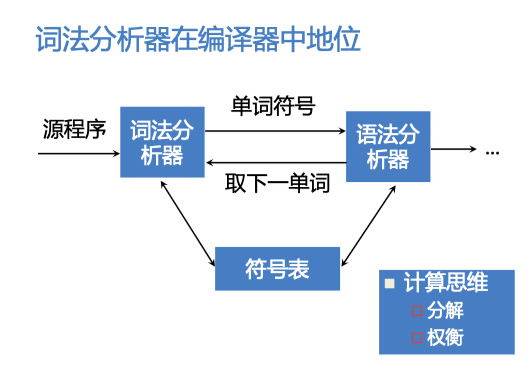
组成:
- 预处理子程序
- 剔除无用空白,回车等
- 扫描器
- 输入缓冲区
- 扫描缓冲区
- 含有起点指示器、搜索指示器
有限自动机
确定有限自动机(DFA)**(Deterministic Finite AutomataDFA):
是一个五元式,表示为状态转换图
可用于确定字符
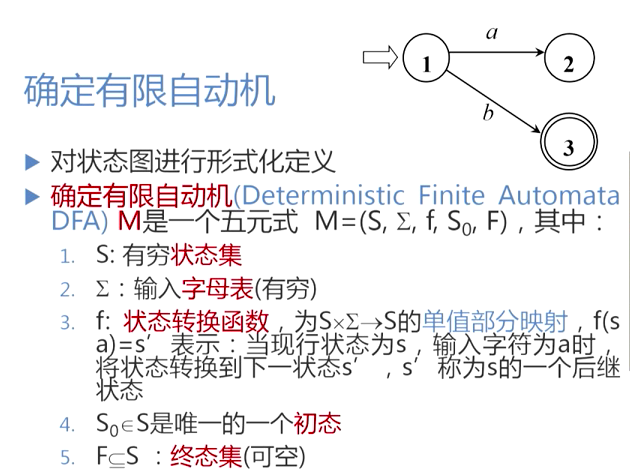
非确定有限自动机(NFA)(Nondeterministic Finite Automata)
表现在转化函数上,转化的结果非确定,可能为一个结果的集合,弧上可为正规式(如AB,A*B)

对于任何两个有限自动机M和M‘,如果L(M)=L(M’),则称二者等价。
NFA和DFA是等价的,可以互相转化。
证明思路:

互相等价关系:
自顶向下分析遇到的问题:
-
回溯问题
- 非终结符含有多个候选,这样需要回溯
消除回溯的解决:
-
文法左递归问题
- $P = P \alpha$,导致语法树无限生长
直接左递归的消除:


使得:
-
不含以$\epsilon$为有部的产生式
-
不含回路
$P \rightarrow^+ P$
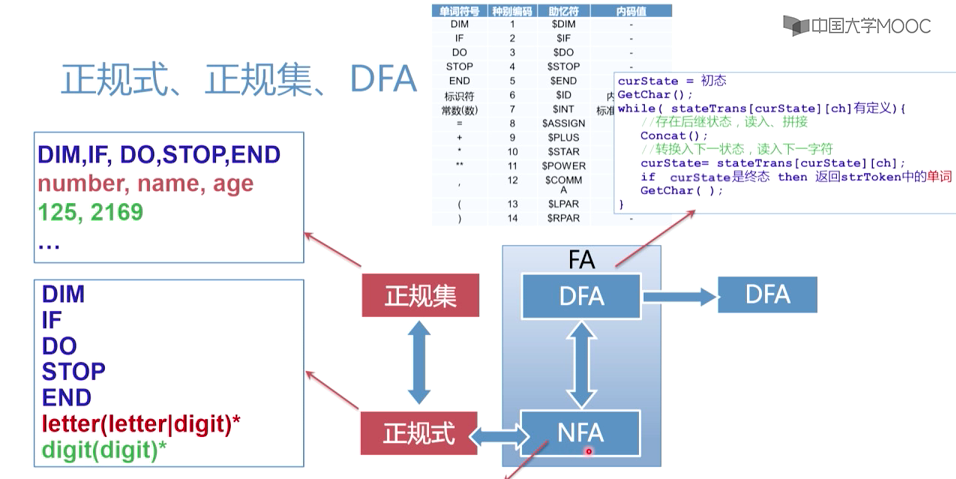
LL(1)分析法

预测分析表的构造思想
对于文法中规则$A \rightarrow \alpha$:
- 放在构造表中$A$所属的行中
- 放在$FIRST(\alpha)$列上
对于文法中规则$A \rightarrow \epsilon $:
- 放在构造表中$A$所属的行中
- 放在$FOLLOW(A)$列上

例题:
LL(1)文法预测分析表
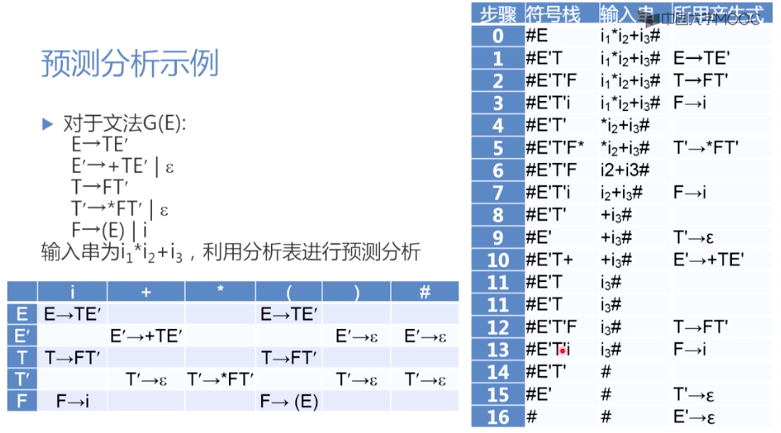
LR(1)文法预测分析表

