ps:持续更新
1. 线性变换和仿射函数定义和区别
P18, P42
定义
线性变换
给定函数$L:R^n\rightarrow R^m$,如果:
- 对于任意$x ∈ R^n $和$a ∈R$,都有$L(ax)=aL(x)$;
- 对于任意$x,y∈R^n$,都有$L(x+y)=L(x)+L(y)$.
那么称函数$L$为一个线性变换
考虑线性变换:$L:R^n \rightarrow R^n$
令$A$为$L$关于${e_1,e_2,···,e_n}$的矩阵表示,$B$为$L$关于${e_1^{‘},e_2^{‘},···,e_n^{‘}}$的矩阵表示。
[$e_1,e_2,···,e_n$]=[$e_1^{‘},e_2^{‘},···,e_n^{‘}$]$T$
令$y=Ax$且$y’=Bx’$,因此有$y’=Ty=TAx=Bx’=BTx$
从而可得$TA=BT$或$A=T^{-1}BT$
结论:给定两个nxn矩阵A和B,如果存在一个非奇异矩阵T,使得$A=T^{-1}BT$,那么称A和B是相似的。在不同的基下,相似矩阵对应的线性变换是相同的
仿射函数
仿射变换是在几何上定义为两个向量空间之间的一个仿射变换或者仿射映射(来自拉丁语,affine,“和…相关”)由一个非奇异的线性变换(运用一次函数进行的变换)接上一个平移变换组成。
如果存在线性函数$L:R^n \rightarrow R^m$和向量$y ∈ R^m$,使得对于任意$x ∈R^n$,都有
那么称函数$A:R^n \rightarrow R^m$是一个仿射函数。
区别
仿射变换=线性变换+平移
材料:
2. $R(A)$和$N(A)$的定义
P21, P312 20.4
令$A ∈ R^{mxn}$
- A的值域空间或者是像空间 $(R(A))$
- 某个空间中所有向量经过变换矩阵后形成的向量的集合
- $R(A) \rightarrow {Ax~:~x \in R^n}$
-
A的零空间$N(A)$,也称作核。
- 所有经过变换矩阵后变成了零向量的向量组成的集合
- ${N(A)\rightarrow {x\in R^n~:~Ax=0}} $
- 所有经过变换矩阵后变成了零向量的向量组成的集合
不管是核还是值域,它们都是封闭的。
3. 梯度、最速下降法(迭代1-2步)
P94 8.1
梯度:是一个矢量,其方向上的方向导数最大,其大小正好是此最大方向导数。
例:利用最速下降法求解函数
\[f(x_1,x_2,x_3)=(x_1-4)^4+(x_2+3)^2+4(x_3+5)^4\]解:
$\nabla f(x)=[4(x_1-4)^3,2(x_2-3),16(x_3+5)^3]$
于是可以算出$\nabla f(x_0)$,算得步长\(\alpha_0=argmin_{a \ge 0}f(x^{(0)}-\alpha\nabla f(x^{(0)}))\),通过函数值最小的时候算得第一个$\alpha_0$,然后更新\(x^{(1)}=x^{(0)}-\alpha_0 \nabla f(x^{(0)})=[4.000,2.008,-5.062]^T\),完成一次迭代
4. 满秩分解和广义逆矩阵
P160 例12.9, P168 例12.10
满秩分解
定义:
矩阵$A \in R^{m\times n},rank~A=r \le min {m,n}$,那么,存在矩阵$B \in R^{m \times r}$和矩阵$C \in R^{r \times n}$,使得 \(A=BC\)
其中, \(rank~A=rank~B=rank~C=r\)
例题:令 \(\begin{equation} A = \left( \begin{array}{cccc} 2 & 1 & -2 & 5 \\ 1 & 0 & -3 & 2 \\ 3 & -1 & -13 & 5 \\ \end{array} \right) \end{equation}\) 求$A$的满秩分解。
解: \(\begin{equation} A = \left( \begin{array}{cccc|ccc} 2 & 1 & -2 & 5 & 1 & 0 & 0 \\ 1 & 0 & -3 & 2 & 0 & 1 & 0 \\ 3 & -1 & -13 & 5 & 0 & 0 & 1 \\ \end{array} \right)\rightarrow \left( \begin{array}{cccc|ccc} 1 & 0 & -1 & 2 &0&1&0\\ 0&1&4&1&1&-2&0\\ 0&0&0&0&1&-5&1\\ \end{array} \right) \end{equation}\) 所以得: \(r(A)=2\\~\\ B= \left( \begin{array}{ccc} 0 & 1 & 0\\ 1 & -2 & 0\\ 1 & -5 & 1\\ \end{array} \right) \\~\\ G= \left( \begin{array}{cccc} 1 & 0 & -3 & 2\\ 0 & 1 & 4 & 1 \end{array} \right)\) 求B的逆矩阵,算$(F|S)$中的$F$ \(B= \left( \begin{array}{ccc} 2 & 1 & 0\\ 1 & 0 & 0\\ 3 & -1 & 1\\ \end{array} \right)=(F\|S) \\~\\ F= \left( \begin{array}{cc} 2 & 1 \\ 1 & 0 \\ 3 & -1 \\ \end{array} \right) (\mbox{因为}r(A)=2)\) 所以 \(A = \left( \begin{array}{cccc} 2 & 1 & -2 & 5 \\ 1 & 0 & -3 & 2 \\ 3 & -1 & -13 & 5 \\ \end{array} \right)=F \times G= \left( \begin{array}{cc} 2 & 1 \\ 1 & 0 \\ 3 & -1 \\ \end{array} \right) \left( \begin{array}{cccc} 1 & 0 & -3 & 2\\ 0 & 1 & 4 & 1 \end{array} \right)\) 分解完毕。
广义逆矩阵
定义:
给定矩阵$A=R^{m \times n}$,如果矩阵$A^{\dagger}\in R^{m \times n}$满足 \(AA^{\dagger}A=A\) 且存在两个矩阵$U\in R^{n\times n},V\in R^{m\times m}$,使得 \(A^\dagger = UA^T \mbox{和} A^\dagger=A^T V\) 则称$A^\dagger$为矩阵A的伪逆。
解题:
给定 \(A = \left( \begin{array}{cccc} 2 & 1 & -2 & 5 \\ 1 & 0 & -3 & 2 \\ 3 & -1 & -13 & 5 \\ \end{array} \right) \mbox{满秩分解分解为B和C,分别为}\\B= \left( \begin{array}{cc} 2 & 1 \\ 1 & 0 \\ 3 & -1 \\ \end{array} \right) \\~\\ C=\left( \begin{array}{cccc} 1 & 0 & -3 & 2\\ 0 & 1 & 4 & 1 \end{array} \right)\) 求A的广义逆矩阵(伪逆矩阵)
解: \(B^\dagger=(B^T B)^{-1}B^T~\mbox{左伪逆}\\ C^\dagger=C^T(CC^T)^{-1}~\mbox{右伪逆}\\ \mbox{所以:}\\ A^{\dagger}=C^\dagger B^\dagger\) 解题完毕。
5. 论述牛顿法-levenberg-marquardt修正原理及其与牛顿法、梯度法之间的关系
P116 9.3节
- 梯度
- $\alpha_0=argmin_\alpha f(x^{(0)}-\alpha\nabla f(x^{(0)}))$
- $\alpha_k=f(x^{(0)}-\alpha\nabla f(x^{(0)}))$
- $x^{(k+1)}=x^{(k)}-\alpha_k g^{(k)}$
- 牛顿法
- $x^{(k+1)}=x^{(k)}-F(x^{k})^{-1}g^{(k)}$
- $g^{(k)}$为$\nabla f(x^k)$
- $F(x)^{-1}$常为黑塞矩阵的逆矩阵
- $x^{(k+1)}=x^{(k)}-F(x^{k})^{-1}g^{(k)}$
- levenberg-marquardt修正
- $x^{(k+1)}=x^{(k)}-(F(x^{(k)})+\mu_k I)^{-1}g^{(k)}$
- 当$\mu_k \rightarrow 0$,修正接近牛顿法
- 当$\mu_k \rightarrow \infin$,步长较小时梯度方法的特性
- 实际应用中,可以先选择较小的值,然后逐渐缓慢添加,知道出现下降的特性
- $x^{(k+1)}=x^{(k)}-(F(x^{(k)})+\mu_k I)^{-1}g^{(k)}$
6. 利用基本的共轭方向算法求解二次型的极小点(迭代1步)
P122 例10.2
针对:n维二次型函数的最小化问题 \(f(x)=\frac{1}{2}x^T Qx-x^T b\) 其中,$Q=Q^T > 0,x\in R^n$。注意,由于$Q>0$,因此函数$f$有一个全局极小点,可通过求解$Qx=b$得到。
例题:
利用基本共轭方向算法求函数 \(f(x_1,x_2)=\frac{1}{2}x^T \left[ \begin{array}{cc} 4 & 2 \\ 2 & 2 \\ \end{array} \right] x-x^T \left[ \begin{array}{c} -1 \\ 1 \end{array} \right] ,x \in R^2\)
初始点为$x^{(0)}=[0,0]^T$,给定$Q$共轭方向为$d^{(0)}=[1,0]^T,d^{(1)}=[\frac{3}{8},\frac{3}{4}]^T$。
解:
需要迭代多少步就有几个共轭方向,并且对于n维的二次型问题,能够在n步之内得到结果
- 需要了解的公式
- $g^{(k)}=Qx^{(k)}-b$
- $\alpha_0=-\frac{g^{(0)T}d^{(0)}}{d^{(0)T}Qd^{(0)}}$
- $x^{(k+1)}=x^{(k)}+\alpha_0d^{(k)}$
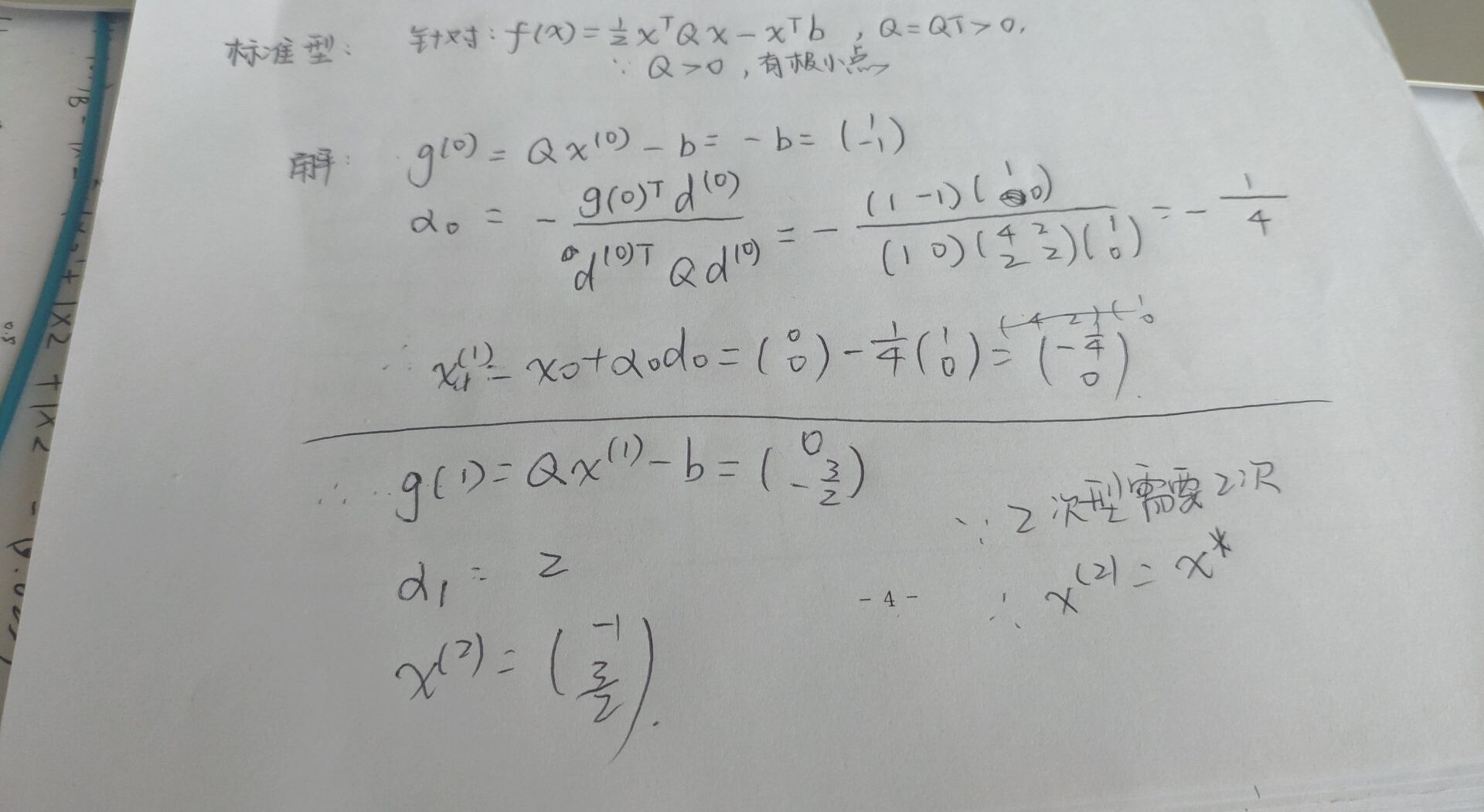
7. 谈谈你对线性规划基本定理的理解
P225 定理15.1
-
如果存在可行解,那么一定存在基本可行解
-
如果存在最优可行解,那么一定存在最优基本可行解
8. 二阶段单纯形法计算
P250 例16.4
题目:
考虑线性规划问题 \(minimize~~~~ ~~2x_1+3x_2 \\ subject~to.~~~~ 4x_1+2x_2 \ge 12 \\ ~~~~~~~~~~~~~~~~~~~~x_1+4x_2 \ge 6 \\ ~~~~~~~~~~~~~~~x_1,x_2 \ge 0\)
-
将问题改写为标准型
-
判断是否有单位矩阵
-
如果有,则直接进行单纯形法求值
-
如果没有,则进行二阶段单纯形法计算
-
第一阶段:判断是否有基本可行解
加入人工变量,构造单位矩阵,进行标准化,即将下方$a_5,a_6$的系数归$0$,求解得 \(\begin{array}{ccccccc} a_1 & a_2 & a_3 & a_4 & a_5 & a_6 & b\\ 4 & 2 & -1 & 0 & 1 & 0 & 12\\ 1 & 4 & 0 & -1 & 0 & 1 & 6\\ -5 & -6 & 1 & 1 & 0 & 0 & -18\\ \end{array}\) 最后算得: \(\begin{array}{ccccccc} a_1 & a_2 & a_3 & a_4 & a_5 & a_6 & b\\ 1 & 0 & -\frac{2}{7} & \frac{1}{7} & \frac{2}{7} & -\frac{1}{7} & \frac{18}{7}\\ 0 & 1 & \frac{1}{14} & -\frac{2}{7} & -\frac{1}{14} & \frac{2}{7} & \frac{6}{7}\\ 0 & 0 & 0 & 0 & 1 & 1 & 0 \end{array}\)
-
9. 简述等式约束条件下,拉格朗日定理结论及其原理
P316-317 定理20.3
拉格朗日定理:
$x^$是$f:R^n \rightarrow R$的局部极小点(或极大点) ,约束条件为$h(x)=0,~h:R^n \rightarrow R^m,~m \le n$。如果$x^$是正则点,那么存在$\lambda^* \in R^m$,使得: \(Df(x^*)+(\lambda^*)^TDh(x^*)=0^T\)
原理:
证明$Df(x^)$和$x^·(t)$正交、$Dh(x^)$与$x^·(t)$正交即可。
方法:构造$h(x(t))$和$f(x(t))$
10. 利用等式约束的拉格朗日条件,求目标函数极值
P319 例20.7
例题:
考虑约束集为椭圆: \(f(x)=x_1^2+x_2^2\) 的优化问题,试求目标函数 \(\{[x_1,x_2]^T~:~h(x)=x_1^2+2x_2^2-1=0\}\) 的极值。
解:


